Oznamy

Plán prednášok a cvičení na zvyšok semestra:

  • Dnes informácie k skúške a posledná ukážka stromov, večer 18:10 semestrálny test.
  • Dnešné cvičenia budú nepovinné.
  • V pondelok 16.12. nepovinná prednáška o nepreberaných črtách jazykov C a C++ (táto nepovinná časť učiva nebude vyžadovaná na skúške, ale môžete ju použiť).
  • V utorok 17.12. v rámci cvičení tréning na skúšku.
    • Na testovači dnes pribudnú tréningové príklady na skúšku. Za niektoré budete môcť získať bonusový bod, ak ich vyriešite do 21.1. (ako tréning sa dajú riešiť aj neskôr). V utorok na cvičeniach pribudne ešte jeden tréningový príklad za 4 body. Ak prídete na cvičenia a odovzdáte na konci aspoň rozumne rozrobenú verziu programu, získate jeden bonusový bod, aj keď ho nestihnete dokončiť.
  • Budúcu stredu nebude prednáška ani cvičenia.
  • V piatok 19.12. od 13:15 predtermín skúšky.

Odporúčame si aspoň raz vyskúšať prácu v Linuxe na školských počítačoch, budete to potrebovať na skúške (./návod).

Prefixové stromy

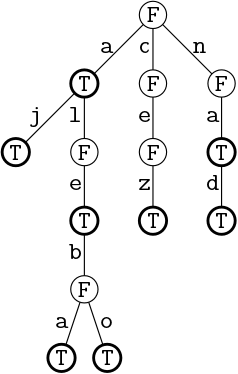
Prefixový strom reprezentujúci množinu reťazcov `a, aj, ale, aleba, alebo, cez, na, nad`.

Prefixové stromy (niekde tiež lexikografické stromy; angl. trie zo slova retrieval) sú dátová štruktúra na uchovávanie množiny reťazcov. Ide o stromy, ktoré nemusia byť binárne:

  • Uzol prefixového stromu má najviac toľko detí, koľko je znakov v uvažovanej abecede. Každé dieťa je označené iným znakom abecedy. Graficky si môžeme predstaviť tento znak prislúchajúci k hrane spájajúcej rodiča a dieťa.
  • Koreň prefixového stromu zodpovedá prázdnemu reťazcu.
  • Uzol v hĺbke k zodpovedá reťazcu dĺžky k, ktorý dostaneme prečítaním písmen na ceste z koreňa do daného uzla.
  • Každý uzol prefixového stromu obsahuje logickú hodnotu vyjadrujúcu, či k nemu prislúchajúci reťazec patrí do množiny reprezentovanej týmto prefixovým stromom.
  • V korektnom prefixovom strome všetky listy zodpovedajú reťazcom z reprezentovanej množiny.
  • Vnútorné vrcholy môžu zodpovedať reťazcu z množiny alebo iba prefixu jedného alebo viacerých takých reťazcov.

Uzly prefixového stromu budeme reprezentovať štruktúrou node

  • Uzol obsahuje obsahuje booleovskú premennú isWord, v ktorej je uložená informácia o tom, či reťazec prislúchajúci k danému uzlu patrí alebo nepatrí do reprezentovanej množiny a pole children smerníkov na jednotlivé deti daného uzla.
  • Veľkosť alphSize tohto poľa je rovná veľkosti uvažovanej abecedy.
  • V ukážkovom programe uvažujeme abecedu ‘a’..’z’.
const int alphSize = 'z' - 'a' + 1;

struct node {
    // pole smerníkov na deti
    node * children[alphSize]; 
    // prislúcha uzol k slovu z množiny?
    bool isWord;              
};

Samotný prefixový strom potrebuje smerník na svoj koreň:

struct trie {
    node * root;      
};

Inicializácia a likvidácia prefixového stromu

Nasledujúca funkcia inicializuje prázdny prefixový strom t:

void init(trie & t) {
    t.root = NULL; 
}

Uvoľnenie pamäte alokovanej pre podstrom zakorenený v uzle root realizujeme obdobne ako pri binárnych vyhľadávacích stromoch. Jediný rozdiel spočíva v potenciálne väčšom počte detí uzla root.

void destroySubtree(node * root) {
    if (root != NULL) {
        for (int i = 0; i < alphSize; i++) {
            destroySubtree(root->children[i]);
        }
        delete root;
    }
}

Nasledujúca funkcia potom zlikviduje celý prefixový strom t:

void destroy(trie & t) {
    destroySubtree(t.root);
}

Hľadanie v prefixovom strome

Funkcia contains pre daný prefixový strom t a reťazec word zistí, či slovo word patrí do množiny reprezentovanej stromom t.

  • Postupuje po písmenách reťazca word. Kým nedôjde na koniec slova, snaží sa ísť po hranách, ktoré zodpovedajú jednotlivým písmenám.
  • V prípade, že v niektorom bode narazí na NULL, slovo word sa v strome nenachádza.
  • V opačnom prípade toto slovo dočíta v nejakom uzle v. V takom prípade slovo word patrí do reprezentovanej množiny práve vtedy, keď v->isWord má hodnotu true.
bool contains(trie & t, const char * word) {
    node * v = t.root;
    if (v == NULL) {
        return false;
    }
    for (int i = 0; word[i] != 0; i++) {
        int c = word[i] - 'a';
        assert(c >= 0 && c < alphSize);
        v = v->children[c];
        if (v == NULL) {
            return false;
        }
    }
    return v->isWord;
}

Vkladanie do prefixového stromu

Pri vkladaní reťazca do množiny reprezentovanej prefixovým stromom potrebujeme vytvárať nové uzly. Túto podúlohu realizuje funkcia createNode, ktorá vytvorí nový uzol s hodnotou isWord danou jej argumentom a so všetkými smerníkmi na deti nastavenými na NULL.

node * createNode(bool isWord) {
    node * v = new node;
    for (int i = 0; i < alphSize; i++) {
        v->children[i] = NULL;
    }
    v->isWord = isWord;
    return v;
}

Vloženie reťazca word do prefixového stromu t vykoná funkcia add, ktorá pracuje nasledovne:

  • Začne v koreni stromu, odkiaľ postupuje nižšie smerom k listom.
  • V každom uzle sa pozrie na ďalšie písmeno slova word. Ak danému uzlu chýba dieťa pre toto písmeno, vytvorí ho pomocou funkcie createNode. Následne sa presunie do tohto dieťaťa.
  • Keď v nejakom uzle v príde na koniec slova word, nastaví hodnotu v->isWord na true.
void add(trie & t, const char * word) {
    if (t.root == NULL) {
        t.root = createNode(false);
    }
    node * v = t.root;
    for (int i = 0; word[i] != 0; i++) {
        int c = word[i] - 'a';
        assert(c >= 0 && c < alphSize);
        if (v->children[c] == NULL) {
            v->children[c] = createNode(false);
        }
        v = v->children[c];
    }
    v->isWord = true;
}

Vymazanie slova z prefixového stromu

Vymazávanie slov z množiny reprezentovanej prefixovým stromom budeme realizovať prostredníctvom pomocnej rekurzívnej funkcie removeFromSubtree.

  • Funkcia z podstromu zakorenenom v uzle root vymaže sufix reťazca word začínajúci na pozícii index.
  • Funkcia vráti booleovskú hodnotu podľa toho, či sa pri tomto vymazaní sufixu z daného podstromu vymazal jeho koreň root.
  • Ak sa slovo word v reprezentovanej množine nenachádza, funkcia removeFromSubtree vyhlási chybu pomocou funkcie assert.

Funkcia removeFromSubtree pracuje nasledovne:

  • Ak je sufix reťazca word začínajúci na indexe index prázdny, nastaví hodnotu root->isWord na false.
  • V opačnom prípade funkcia removeFromSubtree zavolá rekurzívne samú seba pre dieťa zodpovedajúce písmenu na pozícii index reťazca word. Ak toto volanie dané dieťa zmaže, prestaví smerník na toto dieťa na NULL.
  • V prípade, že po vykonaní jednej z predchádzajúcich dvoch operácií nemá uzol root žiadne dieťa a súčasne má root->isWord hodnotu false, uvoľní pamäť alokovanú pre uzol root a informáciu o jeho zmazaní vráti na výstupe.

Cvičenie: hoci mazanie neprehľadáva celý strom, iba jednu cestu z koreňa smerom dolu, naprogramovali sme ho rekurzívne. Na aký problén by sme narazili, ak by sme ju chceli naprogramovať cyklom? Pomohli by nám smerníky na rodiča v uzloch stromu?

bool removeFromSubtree(node * root, 
                       const char * word, int index) {
    assert(root != NULL);
    if (word[index] == 0) {
        assert(root->isWord);
        root->isWord = false;
    } else {
        int c = word[index] - 'a';
        bool deleted = removeFromSubtree(root->children[c], 
                                         word, index + 1);
        if (deleted) {          
            root->children[c] = NULL;
        }
    }
    int numChildren = 0;                        
    for (int i = 0; i < alphSize; i++) {
        if (root->children[i] != NULL) {
            numChildren++;
        }
    }
    if (numChildren == 0 && !root->isWord) {
        delete root;
        return true;
    } else {
        return false;
    }
}

Samotné odstránenie reťazca word z množiny reprezentovanej stromom t potom realizuje funkcia remove.

void remove(trie & t, const char * word) {
    // zavoláme rekurziu pre koreň stromu
    bool rootRemoved = removeFromSubtree(t.root, word, 0);
    // ak bol koreň odstránený, nastavíme t.root na NULL
    if (rootRemoved) {
        t.root = NULL;
    }
}

Výška prefixového stromu

Nasledujúca funkcia vypočíta výšku podstromu zakoreneného v uzle root:

int subtreeHeight(node *root) {
    if (root == NULL) {
        return -1;
    }
    int maxHeight = -1;
    for (int i = 0; i < alphSize; i++) {
        int height = subtreeHeight(root->children[i]);
        if (height > maxHeight) {
            maxHeight = height;
        }
    }
    return maxHeight + 1;
}

Výšku samotného prefixového stromu t potom spočíta nasledujúca funkcia:

int height(trie &t) {
    return subtreeHeight(t.root);
}

Vypisovanie slov reprezentovaných prefixovým stromom

Nasledujúca funkcia printSubtree prehľadáva podstrom zakorenený v uzle root a v reťazci str postupne generuje všetky slová z reprezentovanej množiny, ktoré zároveň vypisuje na konzolu. V parametri index dostane hĺbku aktuálneho vrcholu, t.j. pozíciu v reťazci, na ktorú pridáme ďalší znak.

void printSubtree(node *root, char *str, int index) {
    if (root == NULL) {
        return;
    }
    if (root->isWord) {
        // ukončíme a vypíšeme reťazec
        str[index] = 0; 
        printf("%s\n", str);
    }
    for (int i = 0; i < alphSize; i++) {
        str[index] = 'a' + i;
        printSubtree(root->children[i], str, index + 1);
    }
}

Funkcia printAll vypisujúca všetky slová v množine reprezentovanej prefixovým stromom t najprv spočíta výšku stromu t, ktorá je rovná dĺžke najdlšieho reťazca tejto množiny. Následne dynamicky alokuje reťazec dostatočnej dĺžky na uchovanie každého slova množiny a zavolá funkciu printSubtree pre koreň stromu t.

void printAll(trie &t) {
    int height = height(t);
    if (height >= 0) { 
        char *str = new char[height + 1];
        printSubtree(t.root, str, 0);
        delete[] str;
    }
}

V akom poradí budú slová vypísané?

Ukážka programu s prefixovým stromom, ADT slovník

Na vstupe máme text pozostávajúci zo slov s malými písmenami a pre každé slovo v texte chceme spočítať, koľkokrát sa tam nachádza.

  • Jednotlivé slová uložíme pomocou prefixového stromu a v každom uzle si pamätáme namiesto hodnoty isWord počítadlo count, ktoré udáva, koľkokrát sme príslušné slovo videli na vstupe.
  • Počítadlo má hodnotu nula pre prefixy vstupných slov, ktoré samé zatiaľ ako slovo na vstupe neboli.
  • Namiesto funkcie add máme funkciu increment, ktorá dostane slovo a zvýši jeho počítadlo, pričom ak slovo zatiaľ v strome nebolo, tak ho pridá.
  • Podobne by sme na tento účel vedeli upraviť aj implementáciu množiny pomocou binárneho vyhľadávacieho stromu, hašovacej tabuľky, poľa alebo zoznamu.
    • Pozor, ak sú kľúče reťazce, na ich porovnanie musíme v týchto implementáciách použiť strcmp, nie ==, < a pod.

Abstraktný dátový typ, ktorý si okrem množiny kľúčov ku každému kľúču pamätá aj ďalšie dáta, sa zvykne nazývať slovník (angl. dictionary, map).

  • Tu boli kľúče slová a ďalšie dáta počet výskytov.
  • Iný príklad je zoznam kontaktov, kde kľúčom je meno osoby a pre dané meno chceme vrátiť kontaktné údaje danej osoby (emailová adresa, telefón a pod.)
#include <cstdio>
#include <cassert>
#include <cstring>
using namespace std;

const int alphSize = 'z' - 'a' + 1;

// uzol prefixoveho stromu
struct node {
    // pole smernikov na deti
    node *children[alphSize];
    // pocet vyskytov slova prisluchajuceho uzlu
    int count;
};

// cely prefixovy strom 
struct trie {
    node *root;
};


// inicializacia prazdneho stormu
void init(trie &t) {
    t.root = NULL;
}

// mazanie podstromu s korenom root
void destroySubtree(node *root) {
    if (root != NULL) {
        for (int i = 0; i < alphSize; i++) {
            destroySubtree(root->children[i]);
        }
        delete root;
    }
}

// uvolnenie pamate celeho stromu
void destroy(trie &t) {
    destroySubtree(t.root);
}

// vytvorenie noveho uzlu bez deti a s nula vyskytmi
node *createNode() {
    node *v = new node;
    for (int i = 0; i < alphSize; i++) {
        v->children[i] = NULL;
    }
    v->count = 0;
    return v;
}

// zvysenie pocitadla pre slovo word
// ak slovo este nie je v strome, je pridane
void increment(trie &t, const char *word) {
    if (t.root == NULL) {
        t.root = createNode();
    }
    node *v = t.root;
    for (int i = 0; word[i] != 0; i++) {
        int c = word[i] - 'a';
        assert(c >= 0 && c < alphSize);
        if (v->children[c] == NULL) {
            v->children[c] = createNode();
        }
        v = v->children[c];
    }
    v->count++;
}

// vyska podstromu s korenom root
int subtreeHeight(node *root) {
    if (root == NULL) {
        return -1;
    }
    int maxHeight = -1;
    for (int i = 0; i < alphSize; i++) {
        int height = subtreeHeight(root->children[i]);
        if (height > maxHeight) {
            maxHeight = height;
        }
    }
    return maxHeight + 1;
}

// vyska stromu. t.j. dlzka najdlsieho slova
int height(trie &t) {
    return subtreeHeight(t.root);
}

// vypisanie slov v podstrome prefixoveho stromu
void printSubtree(node *root, char *str, int index) {
    if (root == NULL) {
        return;
    }
    if (root->count > 0) {
        str[index] = 0; // ukoncenie retazca pred vypisom
        printf("%s %d\n", str, root->count);
    }
    for (int i = 0; i < alphSize; i++) {
        str[index] = 'a' + i;
        printSubtree(root->children[i], str, index + 1);
    }
}

// vypisanie slov prefixoveho stromu
void printAll(trie &t) {
    int height = height(t);
    if (height >= 0) {
        char *str = new char[height + 1];
        printSubtree(t.root, str, 0);
        delete[] str;
    }
}

int main() {
    // inicializacia stromu
    trie t;
    init(t);
    // postupne nacitavanie slov
    char word[100];
    while (true) {
        int count = scanf("%99s", word);
        if (count < 1) { // koniec vstupu
            break;
        }
    // pridanie slova resp. zvysenie pocitadla
        increment(t, word);
    }
    // vypis a uvolnenie pamate
    printAll(t);
    destroy(t);
}

Sylaby predmetu

Základy

Konštrukcie jazyka C

  • premenné typov int, double, char, bool, konverzie medzi nimi
  • podmienky (if, else, switch), cykly (for, while)
  • funkcie (a parametre funkcií - odovzdávanie hodnotou, referenciou, smerníkom)
void f1(int x){}            //hodnotou
void f2(int &x){}           //referenciou
void f3(int* x){}           //smerníkom
void f(int a[], int n){}    //polia bez & (ostanú zmeny)
void kresli(Turtle &t){}    //korytnačky, SVGdraw a pod. s &

Polia, reťazce

Reťazec v jazyku C je pole char-ov ukončené nulou.

int A[4]={3, 6, 8, 10}; 
int B[4];               
B[0]=3; B[1]=6; B[2]=8; B[3]=10;

char C[100] = "pes";
char D[100] = {'p', 'e', 's', 0};
  • funkcie strlen, strcpy, strcmp, strcat

Súbory, spracovanie vstupu

  • cin, cout alebo printf, scanf (nekombinovať)
  • fopen, fclose, feof
  • fprintf, fscanf
  • getc, putc, ungetc, fgets, fputs
  • spracovanie súboru po znakoch, po riadkoch, po číslach alebo slovách

Smerníky, dynamicky alokovaná pamäť, dvojrozmerné polia

int i;    // „klasická“ celočíselná premenná
int * p;  // smerník na celočíselnú premennú

p = &i;         // správne
p = &(i + 3);   // zle, i+3 nie je premenná
p = &15;        // zle, konštanta nemá adresu
i = *p;         // správne, ak p bol inicializovaný

int * cislo = new int;  // alokovanie jednej premennej
*cislo = 50;
..
delete cislo;

int a[4];
int *b = a;  // a,b su teraz takmer rovnocenné premenné 

int *b = new int[n]; // alokovanie 1D poľa danej dĺžky
..
delete[] b;

int **a;       // alokovanie 2D matice
a = new int *[n];
for (int i = 0; i < n; i++) a[i] = new int[m];
..
for (int i = 0; i < n; i++) delete[] a[i];
delete[] a;

Abstraktné dátové typy

Abstraktný dátový typ dynamické pole (rastúce pole)

  • operácie init, add, get, set, length

Abstraktný dátový typ dynamická množina (set)

  • operácie init, contains, add, remove
  • implementácie pomocou
    • neutriedeného poľa
    • utriedeného poľa
    • spájaných zoznamov
    • hašovacej tabuľky
    • binárnych vyhľadávacích stromov
    • prefixového stromu (ak kľúč je reťazec)

Abstraktné dátové typy rad a zásobník

  • operácie pre rad (frontu, queue): init, isEmpty, enqueue, dequeue, peek
  • operácie pre zásobník (stack): init, isEmpty, push, pop
  • implementácie: v poli alebo v spájanom zozname
  • využitie: ukladanie dát na spracovanie, odstránenie rekurzie
  • kontrola zátvoriek a vyhodnocovanie výrazov pomocou zásobníka

Dátové štruktúry

Obrázok zoznamu Spájané zoznamy

struct node {
    int data;
    node* next;
};
struct linkedList {
    node* first;
};
void insertFirst(linkedList &z, int d){
    /* do zoznamu z vlozi na zaciatok novy prvok s datami d */
    node* p = new node;   // vytvoríme nový prvok
    p->data = d;          // naplníme dáta
    p->next = z.first;    // uzol ukazuje na doterajší začiatok
    z.first = p;          // tento prvok je novým začiatkom
}

![Strom pre výraz (65 – 3*5)/(2 + 3)](../files/PROG-P21-aritm.png0

Binárne stromy

struct treeNode {
    /* uzol stromu  */
    dataType data;
    treeNode * left;  /* ľavé dieťa */
    treeNode * right; /* pravé dieťa */
};
  • prehľadávanie inorder, preorder, postorder
  • použitie na uloženie aritmetických výrazov

BST Binárne vyhľadávacie stromy

  • vrcholy vľavo od koreňa menší kľúč, vpravo od koreňa väčší
  • contains, add, remove v čase závisiacom od hĺbky stromu

Prefixový strom reprezentujúci množinu reťazcov `a, aj, ale, aleba, alebo, cez, na, nad`. Prefixové stromy

  • ukladajú množinu reťazcov
  • nie sú binárne: vrchol môže mať veľa detí
  • contains, add, remove v čase závisiacom od dĺžky kľúča, ale nie od počtu kľúčov, ktoré už sú v strome
struct node { // uzol prefixoveho stromu 
    bool isWord; // je tento uzol koncom slova?
    node* next[Abeceda]; // pole smernikov na deti    
};

Hašovanie

  • hašovacia tabuľka veľkosti m
  • kľúč k premietneme nejakou funkciou na index v poli {0,…,m-1}
  • každé políčko hašovacej tabuľky spájaný zoznam prvkov, ktoré sa tam zahašovali
  • v ideálnom prípade sa prvky rozhodia pomerne rovnomerne, zoznamy krátke, rýchle hľadanie, vkladenie, mazanie
  • v najhoršom prípade všetky prvky v jednom zozname, pomalé hľadanie a mazanie
int hash(int k, int m){ // veľmi jednoduchá hašovacia funkcia, v praxi väčšinou zložitejšie
    return abs(k) % m;
}
struct node {
    int data;
    node* next;
};

struct set {
    node** data;
    int m;
};

Algoritmy

Rekurzia

  • Rekurzívne funkcie
  • Vykresľovanie fraktálov
  • Prehľadávanie s návratom (backtracking)
  • Vyfarbovanie
  • Prehľadávanie stromov

Triedenia

  • nerekurzívne: Bubblesort, Selectionsort, Insertsort
  • rekurzívne: Mergesort, Quicksort
  • súvisiace algoritmy: binárne vyhľadávanie

Matematické úlohy

  • Euklidov algoritmus, Eratostenovo sito
  • Práca s aritmetickými výrazmi: vyhodnocovanie postfixovej formy, prevod z infixovej do postfixovej, reprezentácia vo forme stromu