Oznamy

Druhý semestrálny test

Prednášky

  • V stredu v prvej polovici prednášky budú informácie k skúške a rady k skúškovému všeobecne, potom doberieme posledné učivo.
  • Budúci pondelok bude nepovinná prednáška o nepreberaných črtách jazykov C a C++.
  • Budúcu stredu prednáška nebude.

Cvičenia

  • Zajtra normálne cvičenia.
  • Túto stredu nepovinné cvičenia bez bonusovej rozcvičky.
  • Budúci utorok v rámci cvičení tréning na skúšku.
  • Budúcu stredu cvičenia nebudú.

Opakovanie: binárne stromy, aritmetický výraz ako strom

Zaoberali sme sa binárnymi stromami, videli sme

  • Terminológiu
  • Štruktúru treeNode
  • Výpis v poradí preorder, inorder, postorder, uvoľnenie pamäte stromu (jednoduchá rekurzia)
  • Hĺbka vrchola a výška stromu

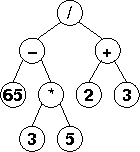
Binárnym stromom môžeme reprezentovať aritmetické výrazy.

  • Vnútorné uzly stromu zodpovedajú operátorom
  • Listy zodpovedajú číselným hodnotám

Strom pre výraz `(65 – 3 * 5)/(2 + 3)`

struct token {
    char op;     // operátor alebo medzera
    double val;  // číselná hodnota
};
typedef token dataType;

/* Uzol binárneho stromu */
struct treeNode {
    // hodnota uložená v uzle
    dataType data;  

    // smerníky na deti
    treeNode * left, * right;
};

Videli sme

  • Vytvorenie stromu z postfixového výrazu (podobné na vyhodnocovanie, využíva sa zásobník hotových podstromov)
  • Vyhodnotenie výrazu, výpis v postfixovej, prefixovej a infixovej forme (jednoduché rekurzívne funkcie)

Binárne vyhľadávacie stromy

Príklad binárneho vyhľadávacieho stromu. Stromy sa v informatike používajú na veľa účelov. Ďalším príkladom sú binárne vyhľadávacie stromy, ktoré môžu slúžiť na implementovanie abstraktného dátového typu dynamická množina, ktorý sme videli na prednáške 14. Prvky množiny nebudeme ukladať do poľa, ani v spájaného zoznamu, ale do vrcholoch binárneho stromu.

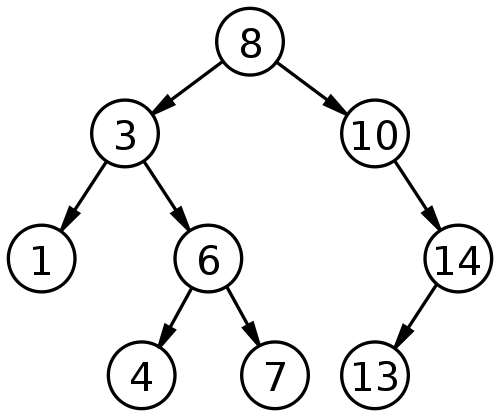
  • V binárnom vyhľadávacom strome má každý vrchol 0, 1 alebo 2 deti
  • V každom vrchole máme položku s dátami, tieto dáta niekedy voláme aj kľúč
  • Pre každý vrchol v stromu platí:
    • Každý vrchol v ľavom podstrome v má hodnotu data menšiu ako vrchol v
    • Každý vrchol v pravom podstrome v má hodnotu data väčšiu ako vrchol v
  • Z toho vyplýva, že ak vypíšeme strom v inorder poradí, dostaneme prvky usporiadané
  • Pre danú množinu kľúčov existuje veľa vyhľadávacích stromov

Cvičenie: nájdite všetky binárne vyhľadávacie stromy pozostávajúce z troch uzlov s kľúčmi 1, 2, 3.

Definícia dátových štruktúr

Vrchol typu treeNode

  • Položka data typu dataType (napr. int alebo iný typ, ktorý vieme porovnávať pomocou <)
  • Smerník na ľavé a pravé dieťa
  • Na niektoré úlohy (napr. mazanie vrcholu) sa hodí aj smerník na rodiča (ten má hodnotu NULL v koreni)

Celý strom je štruktúra obsahujúca iba smerník na koreň

  • Pre prázdny strom je to NULL.
typedef int dataType;
struct treeNode {
    /* vrchol binárneho vyhľadávacieho stromu  */
    dataType data;       /* hodnota uložená vo vrchole */
    treeNode * parent;  /* rodič vrchola, NULL v koreni */
    treeNode * left;    /* ľavé dieťa, NULL ak neexistuje */
    treeNode * right;   /* pravé dieťa, NULL ak neexistuje */
};

/* Samotná dynamická množina (obal pre používateľa). */
struct set {
    treeNode *root;  /* koreň stromu, NULL pre prázdny strom */
};

Inicializácia prázdneho binárneho vyhľadávacieho stromu

/* Funkcia inicializuje prázdny binárny vyhľadávací strom */
void init(set &s) {
    s.root = NULL;
}

Likvidácia binárneho vyhľadávacieho stromu

Likvidáciu podstromu zakoreneného v danom uzle root realizujeme funkciou destroy, obdobne ako pri všeobecných binárnych stromoch. Vytvoríme aj funkciu destroy, ktorá dostane množinu implementovanú ako strom a tento strom zlikviduje.

/* Uvoľní pamäť pre strom s koreňom root */
void destroy(treeNode *root) {
    if (root != NULL) {
        destroy(root->left);
        destroy(root->right);
        delete root;
    }
}

/* Zlikviduje množinu s (uvoľní pamäť) */
void destroy(set &s) {
    destroy(s.root);
}

Hľadanie v binárnom vyhľadávacom strome

Funkcia findNode v podstrome s koreňom root hľadá uzol, ktorého položka dáta obsahuje hľadanú hodnotu x. Vráti takýto uzol alebo NULL ak neexistuje.

  • Najskôr porovná hľadaný kľúč s dátami v koreni:
    • ak sa rovnajú, končíme (našli sme, čo hľadáme),
    • ak je x menšie ako dáta v koreni, musí byť v ľavom podstrome,
    • ak je x väčšie, musí byť v pravom podstrome.
  • V príslušnom podstrome sa rozhodujeme podľa tých istých pravidiel.
  • Keď narazíme na prázdny podstrom, dáta sa v strome nenachádzajú.
  • Dá sa zapísať rekurzívne alebo cyklom, lebo vždy ideme iba do jedného podstromu.

Funkcia contains zavolá funkciu findNode pre koreň daného binárneho vyhľadávacieho stromu t a pomocou nej zistí, či tento strom obsahuje uzol s kľúčom x.

/* Ak v strome s koreňom root existuje uzol s kľúčom x, 
 * vráti ho. Inak vráti NULL. */
treeNode * findNode(treeNode *root, dataType x) {
    treeNode * v = root;
    while (v != NULL && v->data != x) {
        if (x < v->data) {
            v = v->left;
        } else {
            v = v->right;
        }
    }
    return v;
}

/* Rekurzívna verzia */
treeNode *findNodeR(treeNode *root, dataType x) {
    if (root == NULL || x == root->data) {
        return root;
    } else if (x < root->data) {
        return findNodeR(root->left, x);
    } else {  // x > root->data
        return findNodeR(root->right, x);
    }
}

/* Zistí, či strom reprezentujúci množinu s 
 * obsahuje uzol s kľúčom x. */
bool contains(set &s, dataType x) {
    return findNode(s.root, x) != NULL;
}

Čas výpočtu je v najhoršom prípade úmerný výške stromu.

Vkladanie do binárneho vyhľadávacieho stromu

Nasledujúca funkcia insertNode vloží nový uzol s kľúčom x na správne miesto podstromu zakoreneného v *root.

  • Predpokladáme, že prvok v strome nie je.
  • Putujeme po strome podobne ako pri vyhľadávaní prvku, až kým nenarazíme na nulový smerník.
    • Na tomto mieste by mal byť nový prvok, takže ho tam pridáme ako nový list
    • Uvádzame rekurzívnu verziu, ale dá sa aj cyklom, podobne ako pri hľadaní
  • Funkcia add vloží nový uzol pomocou funkcie insertNode ale zvlášť ošetrí prípad, keď ide o prvý uzol.
/* Funkcia vytvorí uzol s daným kľúčom
 * a rodičom, deti nastaví na NULL. */
treeNode * createBSTNode(dataType data, treeNode * parent) {
    treeNode *v = new treeNode;
    v->data = data;
    v->left = NULL;
    v->right = NULL;
    v->parent = parent;
    return v;
}

/* Vloží nový uzol s hodnotou x 
 * na správne miesto stromu s koreňom root */
void insertNode(treeNode *root, dataType x) {
    assert(root != NULL);
    if (x < root->data) {
        if (root->left == NULL) {
            root->left = createBSTNode(x, root);
        } else {
            insertNode(root->left, x);
        }
    } else {
        if (root->right == NULL) {
            root->right = createBSTNode(x, root);
        } else {
            insertNode(root->right, x);
        }
    }
}

/* Vloží do stromu pre množinu s nový uzol s kľúčom x */
void add(set &s, dataType x) {
    if (s.root == NULL) {
        // špeciálny prípad, keď vkladáme prvý uzol
        s.root = createBSTNode(x, NULL);
    } else {
        insertNode(s.root, x);
    }
}

Čas vkladania je tiež v najhoršom prípade úmerný hĺbke stromu.

Cvičenia

  • Ako bude vyzerať strom po nasledujúcej postupnosti operácií?
    set s;
    init(s);
    add(s, 2);
    add(s, 5);
    add(s, 3);
    add(s, 10);
    add(s, 7);
  • Napíšte nerekurzívny variant funkcie insertNode.
  • Do funkcie doplňte assert, ktorý deteguje prípad, že vkladaná hodnota sa už v strome nachádza.
  • V kóde sa trikrát opakuje testovanie smerníka na NULL a podobné riešenie oboch prípadov. Opakovaniu by sme sa vedeli vyhnúť, ak by insertNode fungovala aj pre prázdny strom, pričom by vracala smerník na koreň stromu, do ktorého vložila nový prvok. Ten by sa potom uložil na vhodné miesto. Skúste naprogramovať tento variant. Nezabudnite na nastavovanie rodičov.
  • Napíšte funkciu treeSort, ktorá z poľa celých čísel a pomocou volaní funkcie add vytvorí binárny vyhľadávací strom a následne pomocou prehľadávania tohto stromu v poradí inorder pole a utriedi.

Minimum a následník

Uvedieme teraz dve funkcie, ktoré sa zídu pri mazaní prvku zo stromu, ale môžu sa zísť aj inokedy.

Prvá funkcia minNode nájde vo vyhľadávacom strome uzol, v ktorom je uložená najmenšia hodnota.

  • Všetky prvky menšie ako koreň sú v ľavom podstrome, bude tam zrejme aj minimum.
  • Tá istá úvaha platí pre koreň ľavého podstromu.
  • Ideme teda doľava kým sa dá, posledný vrchol vrátime (list alebo vrchol, ktorý má iba pravé dieťa).
  • Nie je treba teda prechádzať celý strom a nemusíme sa ani pozerať na položku data v uzloch.
  • Dá sa napísať cyklom aj rekurzívne.
  • Obalom pre používateľa bude funkcia min, ktorá pomocou funkcie minNode nájde minimálny kľúč v danej množine.
/* Vráti uzol s minimálnym kľúčom v strome s koreňom v */
treeNode *minNode(treeNode *v) {
    assert(v != NULL);
    while (v->left != NULL) {
        v = v->left;
    }
    return v;
}

/* Vráti minimálnu hodnotu v množine s */
dataType min(set &s) {
    assert(s.root != NULL);
    return minNode(s.root)->data; 
}

Cvičenia:

  • Napíšte rekurzívny variant funkcie minNode.
  • Ako by bolo treba funkciu zmeniť, aby hľadala maximum?

Funkcia successorNode nájde pre daný uzol v jeho následníka (angl. successor) v binárnom vyhľadávacom strome, čiže uzol, ktorý vo vzostupnom poradí podľa kľúčov nasleduje bezprostredne za uzlom v.

  • Ak má uzol v pravé dieťa, následník uzla v bude vrchol s minimálnym kľúčom v pravom podstrome.
  • V opačnom prípade môže byť následníkom uzla v jeho rodič, ak v je jeho ľavé dieťa.
  • Ak je v pravým dieťaťom svojho rodiča, môže to byť jeho prarodič (ak je rodič uzla v ľavým dieťaťom tohto prarodiča), atď.
  • Vo všeobecnosti teda ide o najbližšieho predka uzla v takého, že v patrí do jeho ľavého podstromu.
  • V strome existuje práve jeden uzol bez následníka (najväčší prvok).
    • Ako presne sa bude funkcia nižšie pre tento prvok správať?
/* Vráti uzol, ktorý vo vzostupnom poradí uzlov
 * podľa kľúčov nasleduje za v. 
 * Ak taký uzol neexistuje, vráti NULL. */
treeNode *successorNode(treeNode *v) {
    assert(v != NULL);
    if (v->right != NULL) {
        return minNode(v->right);
    }
    while (v->parent != NULL 
           && v == v->parent->right) {
        v = v->parent;
    }
    return v->parent;
}

Mazanie z binárneho vyhľadávacieho stromu

Nasledujúca funkcia remove zmaže z binárneho vyhľadávacieho stromu uzol s kľúčom x (predpokladá, že taký je).

  • Najprv pomocou funkcie findNode nájde uzol v s kľúčom x.
  • Ak je v list, jednoducho ho zmažeme.
  • Ak má v jedno dieťa, toto dieťa prevesíme priamo pod rodiča v a v zmažeme.
  • Ak má v dve deti, nájdeme nasledovníka v, t.j. minimum v pravom podstrome v.
  • Tento nasledovník nemá ľavé dieťa, vieme ho teda zmazať.
  • Jeho údaje presunieme do vrcholu v.
  • Tiež treba dať pozor na mazanie koreňa.
/* Zmaže zo stromu pre množinu s uzol s kľúčom x */
void remove(set &s, dataType x) {
    // Nájde uzol s hodnotou, ktorú treba vymazať.
    treeNode *v = findNode(s.root, x);
    // Skontrolujme, že požadovaný uzol existuje
    assert(v != NULL);
    
    // Nájde uzol *rm, ktorý sa reálne zmaže
    treeNode *rm;                                          
    if (v->left == NULL || v->right == NULL) {         
        rm = v;
    } else  {
        rm = successorNode(v);
        // Presunie kľúč uzla *rm do uzla *v
        v->data = rm->data;
    }

    // ak má uzol rm dieťa, jeho rodičom bude rodič rm
    treeNode *child;                                      
    if (rm->left != NULL) {
        child = rm->left;
    } else {
        child = rm->right;
    }
    if (child != NULL) {
        child->parent = rm->parent;
    }
    // dieťa rm zavesíme pod rodiča rm
    if (rm->parent == NULL) {
        s.root = child;
    } else if (rm == rm->parent->left) {
        rm->parent->left = child;    
    } else if (rm == rm->parent->right) {
        rm->parent->right = child;
    }
    // rm už nie je v strome, uvoľníme jeho pamäť
    delete rm;
}

Zložitosť jednotlivých operácií

  • Časová zložitosť operácií contains, add aj remove je úmerná výške stromu, ktorú označíme h.
  • Minule sme ukázali, že pre strom s n uzlami máme log2(n+1)-1 ≤ h ≤ n-1.
  • Zložitosť uvedených operácií je teda v najhoršom prípade lineárna od počtu uzlov stromu (tento prípad nastane, ak prvky vkladáme od najmenšieho po najväčší alebo naopak).
  • Dá sa však ukázať, že ak sa prvky vkladajú v náhodnom poradí, výška stromu bude v priemere logaritmická od počtu uzlov.
  • Na predmete Algoritmy a dátové štruktúry (druhý ročník) sa tieto tvrdenia dokazujú poriadne a preberajú sa tam aj varianty vyhľadávacích stromov, pre ktoré je zložitosť uvedených operácií logaritmická aj v najhoršom prípade.

Ukážkový program s binárnymi vyhľadávacími stromami

#include <iostream>
#include <cassert>
using namespace std;

typedef int dataType;

struct treeNode {
    /* vrchol binárneho vyhľadávacieho stromu  */
    dataType data;       /* hodnota uložená vo vrchole */
    treeNode * parent;  /* rodič vrchola, NULL v koreni */
    treeNode * left;    /* ľavé dieťa, NULL ak neexistuje */
    treeNode * right;   /* pravé dieťa, NULL ak neexistuje */
};

/* Samotná dynamická množina (obal pre používateľa). */
struct set {
    treeNode *root;  /* koreň stromu, NULL pre prázdny strom */
};

/* Funkcia inicializuje prázdny binárny vyhľadávací strom */
void init(set &s) {
    s.root = NULL;
}

/* Uvoľní pamäť pre strom s koreňom root */
void destroy(treeNode *root) {
    if (root != NULL) {
        destroy(root->left);
        destroy(root->right);
        delete root;
    }
}

/* Zlikviduje množinu s (uvoľní pamäť) */
void destroy(set &s) {
    destroy(s.root);
}

/* Ak v strome s koreňom root existuje uzol s kľúčom x, 
 * vráti ho. Inak vráti NULL. */
treeNode * findNode(treeNode *root, dataType x) {
    treeNode * v = root;
    while (v != NULL && v->data != x) {
        if (x < v->data) {
            v = v->left;
        } else {
            v = v->right;
        }
    }
    return v;
}

/* Rekurzívna verzia */
treeNode *findNodeR(treeNode *root, dataType x) {
    if (root == NULL || x == root->data) {
        return root;
    } else if (x < root->data) {
        return findNodeR(root->left, x);
    } else {  // x > root->data
        return findNodeR(root->right, x);
    }
}

/* Zistí, či strom reprezentujúci množinu s 
 * obsahuje uzol s kľúčom x. */
bool contains(set &s, dataType x) {
    return findNode(s.root, x) != NULL;
}

/* Funkcia vytvorí uzol s daným kľúčom
 * a rodičom, deti nastaví na NULL. */
treeNode * createBSTNode(dataType data, treeNode * parent) {
    treeNode *v = new treeNode;
    v->data = data;
    v->left = NULL;
    v->right = NULL;
    v->parent = parent;
    return v;
}

/* Vloží nový uzol s hodnotou x 
 * na správne miesto podstromu zakoreneného v root */
void insertNode(treeNode *root, dataType x) {
    assert(root != NULL);
    if (x < root->data) {
        if (root->left == NULL) {
            root->left = createBSTNode(x, root);
        } else {
            insertNode(root->left, x);
        }
    } else {
        if (root->right == NULL) {
            root->right = createBSTNode(x, root);
        } else {
            insertNode(root->right, x);
        }
    }
}

/* Vloží do stromu pre množinu s nový uzol s kľúčom x */
void add(set &s, dataType x) {
    if (s.root == NULL) {
        // špeciálny prípad, keď vkladáme prvý uzol
        s.root = createBSTNode(x, NULL);
    } else {
        insertNode(s.root, x);
    }
}

/* Vráti uzol s minimálnym kľúčom v strome s koreňom v */
treeNode *minNode(treeNode *v) {
    assert(v != NULL);
    while (v->left != NULL) {
        v = v->left;
    }
    return v;
}

/* Vráti minimálnu hodnotu v množine s */
dataType min(set &s) {
    assert(s.root != NULL);
    return minNode(s.root)->data; 
}

/* Vráti uzol, ktorý vo vzostupnom poradí uzlov
 * podľa kľúčov nasleduje za v. 
 * Ak taký uzol neexistuje, vráti NULL. */
treeNode *successorNode(treeNode *v) {
    assert(v != NULL);
    if (v->right != NULL) {
        return minNode(v->right);
    }
    while (v->parent != NULL 
           && v == v->parent->right) {
        v = v->parent;
    }
    return v->parent;
}


/* Zmaže zo stromu pre množinu s uzol s kľúčom x */
void remove(set &s, dataType x) {
    // Nájde uzol s hodnotou, ktorú treba vymazať.
    treeNode *v = findNode(s.root, x);
    // Skontrolujme, že požadovaný uzol existuje
    assert(v != NULL);
    
    // Nájde uzol *rm, ktorý sa reálne zmaže
    treeNode *rm;                                          
    if (v->left == NULL || v->right == NULL) {         
        rm = v;
    } else  {
        rm = successorNode(v);
        // Presunie kľúč uzla *rm do uzla *v
        v->data = rm->data;
    }

    // ak má uzol rm dieťa, jeho rodičom bude rodic rm
    treeNode *child;                                      
    if (rm->left != NULL) {
        child = rm->left;
    } else {
        child = rm->right;
    }
    if (child != NULL) {
        child->parent = rm->parent;
    }
    // dieťa rm zavesíme pod rodiča rm
    if (rm->parent == NULL) {
        s.root = child;
    } else if (rm == rm->parent->left) {
        rm->parent->left = child;    
    } else if (rm == rm->parent->right) {
        rm->parent->right = child;
    }
    // rm už nie je v strome, uvoľníme jeho pamäť
    delete rm;
}

/* Vypíše podstrom s koreňom * root v poradí inorder */
void printInorder(treeNode * root) {
    if (root != NULL) {
        printInorder(root->left);
        cout << " " << root->data;
        printInorder(root->right);
   } 
}

int main() {

    set s;
    init(s);

    cout << "Vkladame 2,5,3,10,7 do s." << endl;
    add(s, 2);
    add(s, 5);
    add(s, 3);
    add(s, 10);
    add(s, 7);  

    cout << "Obsahuje s cisla 2 a 4?" << endl;
    cout << contains(s, 2) << endl;
    cout << contains(s, 4) << endl;

    cout << "Minimum s: " << min(s) << endl;;

    cout << "Vypis v inorder poradi" << endl;
    printInorder(s.root);
    cout << endl;

    cout << "Mazeme 2,5,10 z s." << endl;
    remove(s, 5);
    remove(s, 2);
    remove(s, 10);

    cout << "Vypis v inorder poradi" << endl;
    printInorder(s.root);
    cout << endl;
    
    destroy(s);
}